BudykoTransport¶
digraph inheritance3e5541d9b3 { bgcolor=transparent; rankdir=LR; ratio=expand; size=""; "BudykoTransport" [URL="#climlab.dynamics.budyko_transport.BudykoTransport",dirType=back,fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=14,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="calculates the 1 dimensional heat transport as the difference"]; "EnergyBudget" -> "BudykoTransport" [arrowsize=0.5,dirType=back,style="setlinewidth(0.5)"]; "EnergyBudget" [URL="climlab.process.energy_budget.html#climlab.process.energy_budget.EnergyBudget",dirType=back,fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=14,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A parent class for explicit energy budget processes."]; "TimeDependentProcess" -> "EnergyBudget" [arrowsize=0.5,dirType=back,style="setlinewidth(0.5)"]; "Process" [URL="climlab.process.process.html#climlab.process.process.Process",dirType=back,fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=14,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A generic parent class for all climlab process objects."]; "TimeDependentProcess" [URL="climlab.process.time_dependent_process.html#climlab.process.time_dependent_process.TimeDependentProcess",dirType=back,fillcolor=white,fontname="Vera Sans, DejaVu Sans, Liberation Sans, Arial, Helvetica, sans",fontsize=14,height=0.25,shape=box,style="setlinewidth(0.5),filled",target="_top",tooltip="A generic parent class for all time-dependent processes."]; "Process" -> "TimeDependentProcess" [arrowsize=0.5,dirType=back,style="setlinewidth(0.5)"]; }- class climlab.dynamics.budyko_transport.BudykoTransport(b=3.81, **kwargs)[source]¶
Bases:
EnergyBudgetcalculates the 1 dimensional heat transport as the difference between the local temperature and the global mean temperature.
- Parameters:
b (float) – budyko transport parameter n - unit: \(\\textrm{W} / \\left( \\textrm{m}^2 \\ ^{\circ} \\textrm{C} \\right)\) n - default value:
3.81
As BudykoTransport is a
Processit needs a state do be defined on. See example for details.Computation Details: n
In a global Energy Balance Model
\[\begin{split}C \\frac{dT}{dt} = R\downarrow - R\uparrow - H\end{split}\]with model state \(T\), the energy transport term \(H\) can be described as
\[\begin{split}H = b [T - \\bar{T}]\end{split}\]where \(T\) is a vector of the model temperature and \(\\bar{T}\) describes the mean value of \(T\).
For further information see [].
- Example:
Budyko Transport as a standalone process:
import climlab from climlab.dynamics.budyko_transport import BudykoTransport from climlab import domain from climlab.domain import field from climlab.utils.legendre import P2 import numpy as np import matplotlib.pyplot as plt # create domain sfc = domain.zonal_mean_surface(num_lat = 36) lat = sfc.lat.points lat_rad = np.deg2rad(lat) # define initial temperature distribution T0 = 15. T2 = -20. Ts = field.Field(T0 + T2 * P2(np.sin(lat_rad)), domain=sfc) # create BudykoTransport process budyko_transp = BudykoTransport(state=Ts) ### Integrate & Plot ### fig = plt.figure( figsize=(6,4)) ax = fig.add_subplot(111) for i in np.arange(0,3,1): ax.plot(lat, budyko_transp.default, label='day %s' % (i*40)) budyko_transp.integrate_days(40.) ax.set_title('Standalone Budyko Transport') ax.set_xlabel('latitude') ax.set_xticks([-90,-60,-30,0,30,60,90]) ax.set_ylabel('temperature ($^{\circ}$C)') ax.legend(loc='best') plt.show()
(
Source code,png,hires.png,pdf)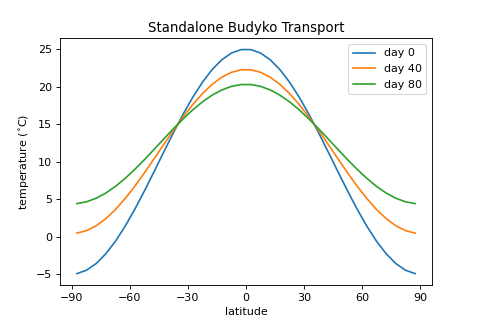
- Attributes:
bthe budyko transport parameter in unit
depthDepth at grid centers (m)
depth_boundsDepth at grid interfaces (m)
diagnosticsDictionary access to all diagnostic variables
inputDictionary access to all input variables
latLatitude of grid centers (degrees North)
lat_boundsLatitude of grid interfaces (degrees North)
levPressure levels at grid centers (hPa or mb)
lev_boundsPressure levels at grid interfaces (hPa or mb)
lonLongitude of grid centers (degrees)
lon_boundsLongitude of grid interfaces (degrees)
timestepThe amount of time over which
step_forward()is integrating in unit seconds.
Methods
add_diagnostic(name[, value])Create a new diagnostic variable called
namefor this process and initialize it with the givenvalue.add_input(name[, value])Create a new input variable called
namefor this process and initialize it with the givenvalue.add_subprocess(name, proc)Adds a single subprocess to this process.
add_subprocesses(procdict)Adds a dictionary of subproceses to this process.
compute()Computes the tendencies for all state variables given current state and specified input.
compute_diagnostics([num_iter])Compute all tendencies and diagnostics, but don't update model state.
declare_diagnostics(diaglist)Add the variable names in
inputlistto the list of diagnostics.declare_input(inputlist)Add the variable names in
inputlistto the list of necessary inputs.integrate_converge([crit, verbose])Integrates the model until model states are converging.
integrate_days([days, verbose])Integrates the model forward for a specified number of days.
integrate_years([years, verbose])Integrates the model by a given number of years.
remove_diagnostic(name)Removes a diagnostic from the
process.diagnosticdictionary and also delete the associated process attribute.remove_subprocess(name[, verbose])Removes a single subprocess from this process.
set_state(name, value)Sets the variable
nameto a new statevalue.set_timestep([timestep, num_steps_per_year])Calculates the timestep in unit seconds and calls the setter function of
timestep()step_forward()Updates state variables with computed tendencies.
to_xarray([diagnostics])Convert process variables to
xarray.Datasetformat.
